pcb线路板设计中滤波器是任何工程师都必须理解的关键电路,它们具有简单的数学表示形式,可帮助设计人员可视化其功能。作为滤波器设计,仿真和评估的一部分,波特图是用于可视化谐波输入的滤波器输出的基本工具。尤其是对于线性时不变(LTI)系统,波特图显示了电路的传递函数,这是仿真PCB和集成电路中因果系统的基本部分。
可以由简单的无源电路元件构成的一种基本滤波器是带通滤波器。如果系统的电阻足够大,则带通滤波器的波特图的图形可以转变为低通行为,这是可以从视觉上看到的滤波器的一个方面。这是如何解释和使用带通滤波器的波特图以及简单电路的示例。
建立带通滤波器波特图
伯德图只是电路传递函数的对数图。这包括带通滤波器的波特图,可用于查看系统的谐振或非谐振行为。可以从过滤器的Bode图确定一些重要点:
增益和衰减:具有增益的线性电路,例如以线性方式工作的运算放大器或接近谐振的带通滤波器,其输出将大于输入(对数刻度为正dB值),反之反之亦然。这可以在波特图中轻松看出。
共振,带宽和衰减:通过观察传递函数的大小可以看出这些特征,如波特图所示。谐振仅在特定带宽内发生,该带宽可用于计算电路的Q因子。另外,系统的响应在带宽限制(通常被视为-3dB频率)之上和/或之下具有一定的衰减。
相移或反转:在Bode图的相位部分中查看,它将显示输出的相位与输入的相位如何相关。这对于与驱动器串联匹配的传输线非常重要。从输出中提取出相位延迟后,线路传递函数的伯德图就会显示出在存在阻抗失配的情况下,不同频率下会发生谐振。
电路的传递函数可以使用基尔霍夫定律和欧姆定律手动计算,也可以通过SPICE仿真确定。请注意,传递函数仅为LTI系统定义,尽管有大量关于传递函数的非线性时间相关表示的研究文献。对于带通滤波器之类的简单线性电路,可以很容易地计算出波特图,如以下示例所示。
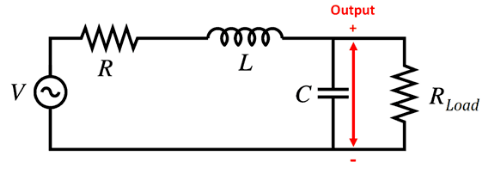
串联RLC电路示例
也许可以构造的最简单的带通电路是串联RLC谐振电路,其中电阻,电容器和电感器串联放置。该电路在较窄的带宽内具有增益的带通特性。信号的最大增益和相位取决于该网络中电阻的值。最后,该电路的输出(通常跨接电容器)可以连接到负载组件。然后,负载阻抗确定系统中的确切传递函数,可以在伯德图中将其可视化。
下面的电路显示了串联RLC电路的示例,其输出连接到20欧姆负载电阻。负载与电容器并联布置,即滤波器的输出跨接电容器。串联电阻R将确定电路中的阻尼水平和电路的传递函数,以及传递给负载的总功率。
具有20Ohm负载的简单串联RLC带通滤波器电路
下面的带通滤波器Bode图显示了当串联电阻R的各种值发生谐振时的情况。我们可以看到在R=0.2Ohms时发生强烈谐振,这是可以预期的,因为电路中的阻尼与R成正比。的R,我们看到低通滤波器的行为;这是因为电容器在低频时将具有最高阻抗,因此所有输入电压将在电容器和负载电阻两端下降。我们还可以看到,相位反转发生在谐振频率之外,即输出和输入几乎完全异相。
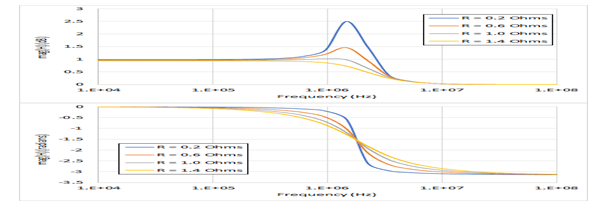
串联RLC电路的带通滤波器Bode图,输出通过电容器
尽管在此示例中,输出跨接在电容器两端,但也可以跨接在电感器两端。在这种情况下,我们仍然会在电路的固有频率上产生谐振。此外,在谐振频率以上,我们将具有高通特性,而在低频处,则具有相同类型的相位反转。在高频下,输出电压和输入电压完全同相。从欧姆定律可以预料到这一点,即,由于电感具有最大的阻抗,所有电压会在电感两端下降。
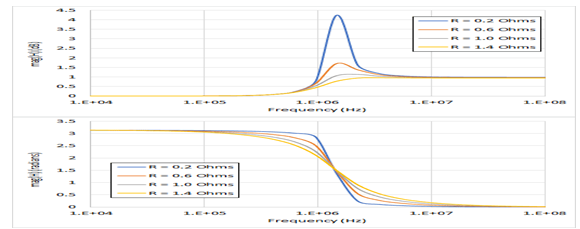
串联RLC电路的带通滤波器Bode图,其中输出跨接电感器
从这两个曲线图中,我们了解到串联RLC电路及其在Bode曲线中看到的相位反转的一些重要知识:零输出电压与输入电压相比,对应于输出电压的完全相位反转。换句话说,输入和输出电压产生相消干扰并相互抵消。这就是为什么在每种配置中,在特定频率范围内,负载电阻两端不会消耗功率的原因。



